Material: Cotton cloth
Robert A. Heinlein’s 1941 science fiction short story ”…And He Built a Crooked House“ introduces a house built in the shape of a 3-dimensional unfolding of a hypercube. As a result of an earthquake, the house folds ‘up’ to an actual 4D hypercube, and the inhabitants are trapped inside. Like ants walking around the surface of a cube from square to square, they navigate the eight cubical rooms of the house taking straight-line routes northeast to southwest, southeast to northwest, up and down, only to find themselves back were they started from after a round trip.
Such investigations can be facilitated with hand-held kinetic artefacts that employ hyperbolic patchwork surfaces based on the truncated versions of regular polychora. For the purpose of the patchwork surface models, we truncate the pentachoron and the hypercube all the way to their bitruncated form, where the cells resulting from the truncation have started to truncate each other.
When the pentachoron (5 vertices, 10 edges, 10 triangular faces, 5 tetrahedral cells) is bitruncated, the result is a polychoron composed of 10 truncated tetrahedra. In the object called Crooked House I the triangular faces are removed, and the remaining 20 hexagons form a closed surface hyperbolic at the vertices with 4 hexagons meeting at a them. The cells of the bitruncated pentachoron are connected to each other via triangular openings. Topologically it is a torus with six handles.

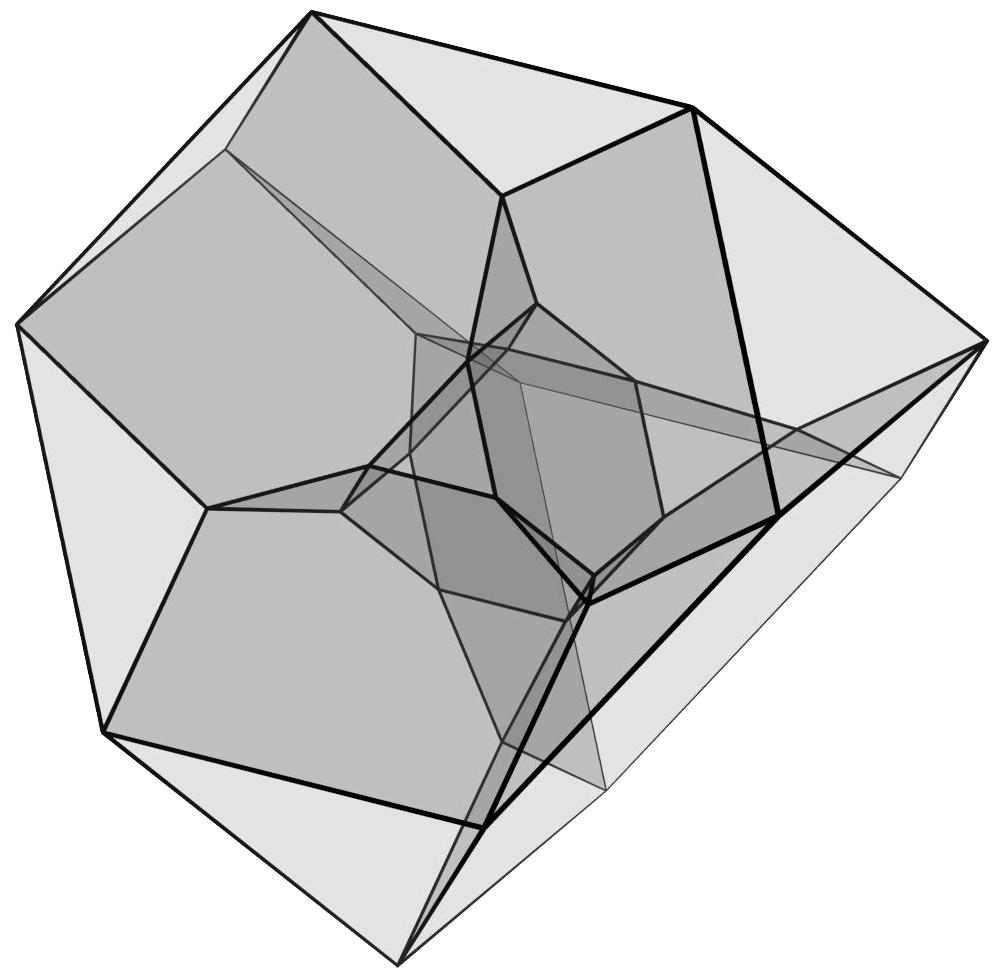
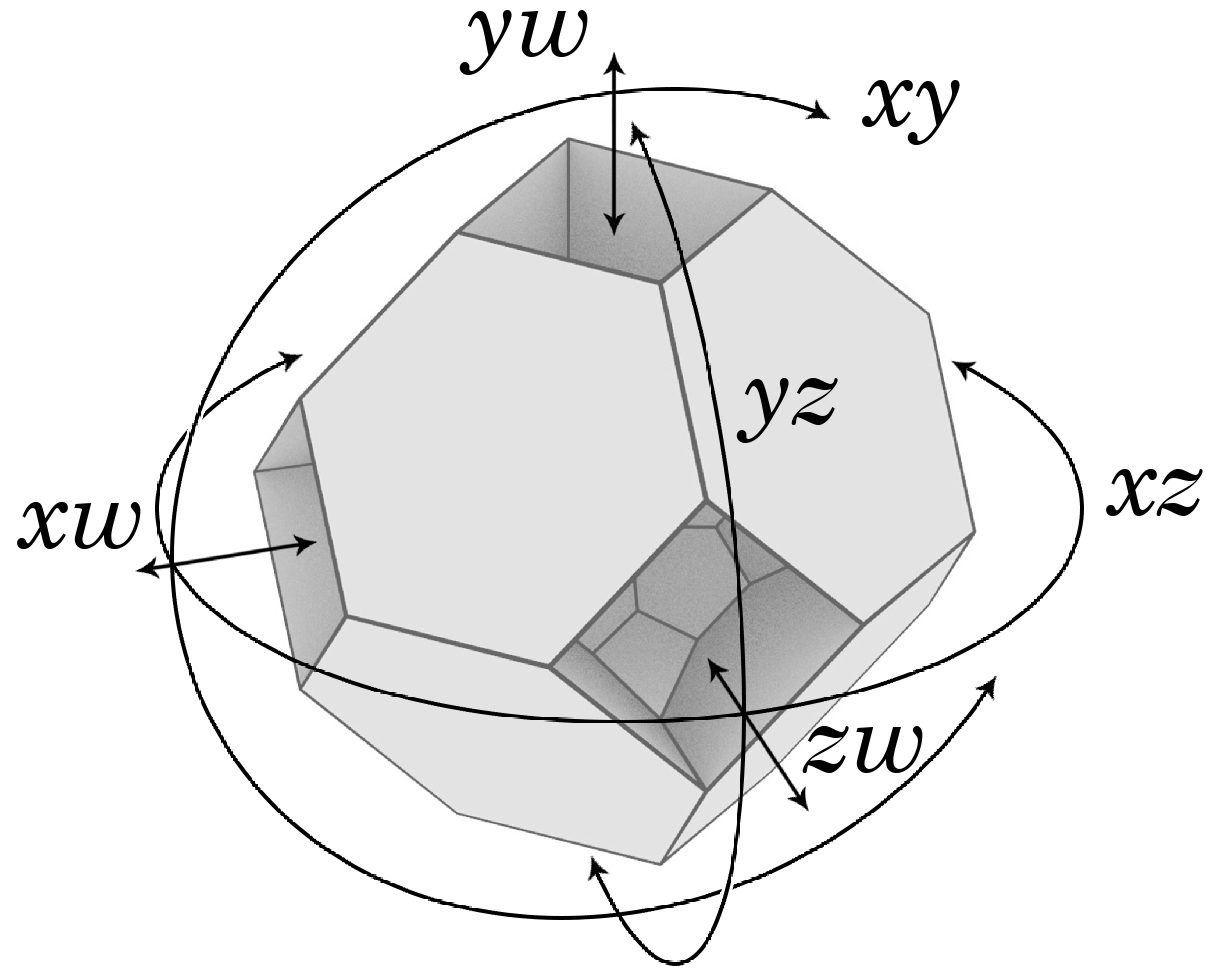
When the hypercube (16 vertices, 32 edges, 24 square faces, 8 cubical cells) is bitruncated, the result is a polychoron composed of 8 truncated octahedra corresponding to the original cells of the hypercube, and 16 truncated tetrahedra corresponding to the original vertices of the hypercube.
In the object Crooked House II a.k.a. the Hyper–Diaper, the square faces are removed, leaving us with a closed surface composed of 64 hexagons. As the hexagons meet 4 per vertex, the surface is hyperbolic at the vertices. This surface is topologically a torus with 17 handles.